YPEA: Yarpiz Evolutionary Algorithms

YPEA for MATLAB [+] is a general-purpose toolbox to define and solve optimization problems using Evolutionary Algorithms (EAs) and Metaheuristics. To use this toolbox, you just need to define your optimization problem and then, give the problem to one of the algorithms provided by YPEA, to get it solved.

List of Provided Algorithms

Currently, YPEA supports these algorithms to solve optimization problems. The list is sorted in alphabetic order.

1. Artificial Bee Colony (ABC)
2. Ant Colony Optimization for Continuous Domains (ACOR)
3. Bees Algorithm (BA)
4. Biogeography-based Optimization (BBO)
5. Covariance Matrix Adaptation Evolution Strategy (CMA-ES)
6. Cultural Algorithm (CA)
7. Differential Evolution (DE)
8. Firefly Algorithm (FA)
9. Genetic Algorithm (GA)
10. Harmony Search (HS)
11. Imperialist Competitive Algorithm (ICA)
12. Invasive Weed Optimization (IWO)
13. Particle Swarm Optimization (PSO)
14. Simulated Annealing (SA)
15. Teaching-Learning-based Optimization (TLBO)

Installation

A MATLAB toolbox package file (*.mltbx) is available in the dist folder. You can right-click on this file inside MATLAB, and select the Install option to get it installed on your machine. This is the recommended way of installing YEPA.

However, if you prefer, the source code for YPEA is available in src folder, and you can download it and add the ypea folder to the path of your MATLAB installation.

The toolbox has its own documentation, which is accessible via the MATLAB documentation center. You may find it under the Supplemental Software section of MATLAB documentation center. To access the documentation from the command line, type doc ypea. The documentation for the toolbox will be shown.

How YPEA Works?

The main steps to set up your problem and solve it using YPEA are listed below:

1. Define Optimization Problem

   • Initialize an instance of the optimization problem
   • Set the type of optimization problem (either minimization or maximization)
   • Define search space and decision variables
   • Define the objective function
     • Note: In the case of the constrained optimization problem, constraints are defined and using methods like penalty functions, they are incorporated into the final objective function.

2. Use Optimization Algorithm

   • Create an instance of optimization algorithm class
   • Set the parameters of algorithms
   • Call solve method of the algorithm, passing the problem object into it
   • Get the optimization results and visualize (if needed to do so)

A Classic Example

Problem Definition

Assume that we would like to find 20 real numbers in the range [-10,10], which minimize the value of the well-known sphere function, defined by:

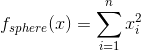
To define this problem, we run these commands in MATLAB:

problem = ypea_problem();

problem.type = 'min';

problem.vars = ypea_var('x', 'real', 'size', 20, 'lower_bound', -10, 'upper_bound', 10);

sphere = ypea_test_function('sphere');

problem.obj_func = @(sol) sphere(sol.x);

Particle Swarm Optimization (PSO)

Now, we are ready to use any of the algorithms available in YPEA to solve the problem we just defined. Here we are going to use Particle Swarm Optimization (PSO). Let’s create an instance of PSO (ypea_pso) and set its parameters.

pso = ypea_pso();

pso.max_iter = 100;
pso.pop_size = 100;

pso.w = 0.5;
pso.wdamp = 1;
pso.c1 = 1;
pso.c2 = 2;

One may use so-called Constriction Coefficients for PSO, by running these commands:

phi1 = 2.05;
phi2 = 2.05;
pso.use_constriction_coeffs(phi1, phi2);

Now, we are ready to get our problem solved. Let’s call the solve method of PSO:

pso_best_sol = pso.solve(problem);

The best solution found by PSO is accessible via:

pso_best_sol.solution.x

Differential Evolution (DE)

It is possible to pass the problem to another algorithm to get it solved. For example, if we would like to use Differential Evolution (DE), we can create an instance of DE (ypea_de) and set its parameters. Assume that we are using the DE/best/2/bin, which means:

• using the best solution ever found as the base vector,
• using two difference vectors for mutations (creating the trial vector),
• and using the binary method for crossover.

de = ypea_de('DE/best/2/bin');

de.max_iter = 1000;
de.pop_size = 20;

de.beta_min = 0.1;
de.beta_max = 0.9;
de.crossover_prob = 0.1;

By calling the solve method of DE and passing the problem into it, we can solve the optimization problem:

de_best_sol = de.solve(problem);

The best solution found by Differential Evolution is given by:

de_best_sol.solution.x

Types of Decision Variables

One of the difficulties in modeling and defining optimization problems is dealing with different kinds of decision variables. In YPEA, there several types of decision variables are supported and make the problem definition much easier.

Supported variable types in YPEA, are listed below:

• Real Variables, which are used to model real-valued (continuous) variables, in any size (scalar, vector, matrix, etc.), with any combination of lower and upper bounds.
  • Sample usage: most real-world mathematical programming and optimization problems.
• Integer Variables, which are used to model integer-valued (discrete) variables, in any size (scalar, vector, matrix, etc.), with any combination of lower and upper bounds.
  • Sample usage: Generalized Knapsack Problem.
• Binary Variables, which are a special case of integer variables, with lower bound set to 0, and upper bound set to 1;
  • Sample usage: Standard (Binary) Knapsack Problem.
• Permutation Variables, which are used to model permutations of some items, and can include more than one permutation per variable (as rows of a matrix).
  • Sample usage: Traveling Salesman Problem (TSP), n-Queens Problem, and Quadratic Assignment Problem (QAP).
• Selection Variables, which are used to model fixed-length selections of some items, and can include more than one selection per variable (as rows of a matrix).
  • Sample usage: Feature Selection.
• Partition/Allocation Variables, which are used to partition a list of items into disjoint subsets (also known as allocation and assignment), and can include more than one partitioning per variable (as rows of matrices).
  • Sample usage: Vehicle Routing Problem (VRP) and Hub Location Allocation.
• Fixed Sum Variables, which are used to model real-valued variables that are needed to have some fixed target sum value (in the whole matrix, in rows, or in columns).
  • Sample usage: Transportation Problem.

All of these variable types are encoded to real values in the range of [0,1]. Hence, all of the algorithms implemented in YPEA, can be used to solve any defined problem, interchangeably.

Project’s Github Repository [+]

Downloads

The download links of this project are listed below.

Citing This Work

If you wish, you can cite this content as follows.